
Since the last article on “Using Prolog to Solve Logic Puzzles” 4 years ago, I finally woke up and discovered how to use the amazing clp(fd) - Constraint Logic Programming (Finite Domain) module. Various implementation of clp(fd) existed in different Prolog dialects but the concepts are essentially shared. To illustrate how clp(fd) is a perfect fit for many combinatorics problems, we shall explore by using SWI Prolog implementation of clp(fd) to solve a few types of logic puzzle.
Constraint logic programming is naturally fit into the paradigm for logic languages like Prolog, in which “relations between variables are stated in the form of constraints.” For instance, the following expressions:
The term “Finite Domain” is just a fancy way of saying all numbers \(\in \mathbb\). If we can transform a puzzle into Integers, clp(fd) can be applied to transform the puzzle into an efficient combinatorics search problem.
Since clp(fd) is not loaded when SWI Prolog started, you can simply import the module by,
:- use_module(library(clpfd). As a learning exercise, we have converted 3 types of commonly known logic puzzles,
These can be elegantly and efficiently solved with Prolog and constraints. The first 2 types of puzzles (1) Cryptarithmetic Puzzle and (2) Logic Puzzle can be very directly modelled and solved as combinatorial tasks. The third type (3) Spatial Logic Puzzle needs more effort to find a suitable formulation as such tasks. After encoding all of these puzzles as integers, Prolog constraints can search over the different states efficiently.
The classical SEND + MORE = MONEY cryptarithmetic puzzle constrained the assignment of letters between the digits 0 thru 9. They spell out “SEND MORE MONEY” and when read as base 10 numbers create a true mathematical formula. An additional constraint is the leading letter is not permitted to be zero.
Here is another similar cryptarithmetic puzzle of FORTY + TEN + TEN = SIXTY that we shall solve here.

Using clp(fd), the solution is naturally expressed in the specified constraints [CLPFD-TUTOR],
:- use_module(library(clpfd)). puzzle_sixty([F,O,R,T,Y] + [T,E,N] + [T,E,N] = [S,I,X,T,Y]) :- Vars = [F,O,R,T,Y,E,N,S,I,X], Vars ins 0..9, all_different(Vars), F*10000 + O*1000 + R*100 + T*10 + Y + 2*(T*100 + E*10 + N) #= S*10000 + I*1000 + X*100 + T*10 + Y, F #\= 0, T #\= 0, S #\= 0, label(Vars). Starting the SWI Prolog and import the puzzles.pl file,
$ swipl ?- [puzzles]. true. ?- puzzle_sixty(X). X = ([2, 9, 7, 8, 6]+[8, 5, 0]+[8, 5, 0]=[3, 1, 4, 8, 6]) ; false. There are rooms for improvement, for instance, since the letter position defines the digit multiplier of 10s, for example, “FORTY” is expressed as,
F*10000 + O*1000 + R*100 + T*10 + Y This is not ideal and error prone to write. We can generalize by defining the relation between a list of digits and the represented number:
digits_number(Ds, N) :- length(Ds, _), Ds ins 0..9, reverse(Ds, RDs), foldl(pow, RDs, 0-0, N-_). pow(D, N0-I0, N-I) :- N #= N0 + D*10^I0, I #= I0 + 1. Then, we can convert to use the digits_number/2 relation to make the program read more elegantly,
:- use_module(library(clpfd)). puzzle_sixty_new([F,O,R,T,Y] + [T,E,N] + [T,E,N] = [S,I,X,T,Y]) :- Vars = [F,O,R,T,Y,E,N,S,I,X], Vars ins 0..9, all_different(Vars), digits_number([F,O,R,T,Y], FORTY), digits_number([T,E,N], TEN), digits_number([S,I,X,T,Y], SIXTY), FORTY + 2 * TEN #= SIXTY, F #\= 0, T #\= 0, S #\= 0, label(Vars). As expected, the solution should be the same as before.
?- puzzle_sixty_new(X). X = ([2, 9, 7, 8, 6]+[8, 5, 0]+[8, 5, 0]=[3, 1, 4, 8, 6]) . We can also revisit the Zebra Puzzle using the constructs of constraint programming. Just for convenience, we shall repeat the puzzle and then we can provide a solution by using clp(fd) [CLPFD-PUZZLE].
The Zebra Puzzle comes with 15 facts and 2 questions: Who has a zebra and who drinks water?

The list of facts (or constraints):
The clp(fd) formulation will be [CLPFD-PUZZLE],
zebra_puzzle(Pairs, Water, Zebra, Vs) :- Table = [Houses,Nations,Drinks,Smokes,Animals], Houses = [Red,Green,Yellow,Blue,Ivory], Nations = [England,Spain,Ukraine,Norway,Japan], Names = [england,spain,ukraine,norway,japan], Drinks = [Coffee,Milk,OrangeJuice,Tea,Water], Smokes = [OldGold,Kools,Chesterfield,LuckyStrike,Parliaments], Animals = [Dog,Snails,Horse,Fox,Zebra], pairs_keys_values(Pairs, Nations, Names), maplist(all_distinct, Table), append(Table, Vs), Vs ins 1..5, England #= Red, % hint 2 Spain #= Dog, % hint 3 Coffee #= Green, % hint 4 Ukraine #= Tea, % hint 5 Green #= Ivory + 1, % hint 6 OldGold #= Snails, % hint 7 Kools #= Yellow, % hint 8 Milk #= 3, % hint 9 Norway #= 1, % hint 10 next_to(Chesterfield, Fox), % hint 11 next_to(Kools, Horse), % hint 12 LuckyStrike #= OrangeJuice, % hint 13 Japan #= Parliaments, % hint 14 next_to(Norway, Blue). % hint 15 next_to(H, N) :- abs(H-N) #= 1. After studying Markus’s solution using clp(fd), I immediately fall in love with the directness of translating the puzzle hints into the constraint relations. Although clp(fd) allows the domain to be expressed as the house label directly, mapping the house labels to an integer will enhance the ability for clp to optimize the search efficiently. Each house will be mapped as an integer in . Also, I want to point out the elegant way of representing H neighbouring house N relation by using the constraint such that the absolute positional difference must be 1.
abs(H-N) #= 1 This relation works correctly in all directions, no matter which of the two variables, if any, is already instantiated. Thus, translating such puzzles to integers often increases convenience when expressing the desired relations, and often also improves performance due to pruning techniques that are automatically applied. In addition, keeping your programs pure lets you benefit from powerful additional techniques such as declarative debugging.
Using labeling, we obtain the puzzle’s unique solution:
?- zebra_puzzle(Pairs, Water, Zebra, Vs), label(Vs). Pairs = [3-england, 4-spain, 2-ukraine, 1-norway, 5-japan], Water = 1, Zebra = 5, Vs = [3, 5, 1, 2, 4, 3, 4, 2, 1|. ] ; false. The previous article on “Spatial Reasoning Explained” presented a typical spatial logic puzzle that is often found in the puzzle books. We described a solution using a spatial topological network of houses to support their directional relations (e.g. east, west, north, south). Now, we shall revisit the problem by using clp(fd) to solve this house puzzle.
The puzzle states that five married couples live in houses shown on the map below.
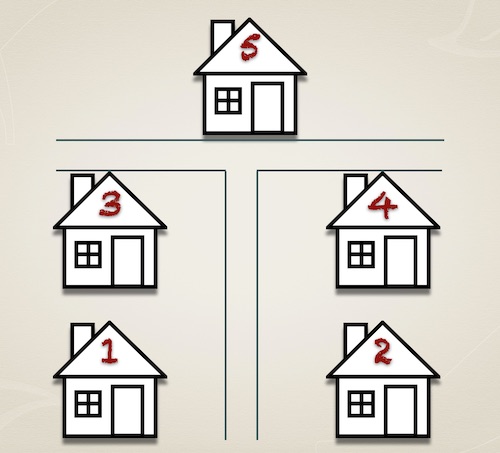
For using clp(fd), we need to take one more step to translate the house’s topological relations (east, west, north, south) into Integer domain. By overlaying a grid onto the map, we can describe the house position as (X,Y) coordinate; subsequently translated to X-Y integer pairs as constraints.
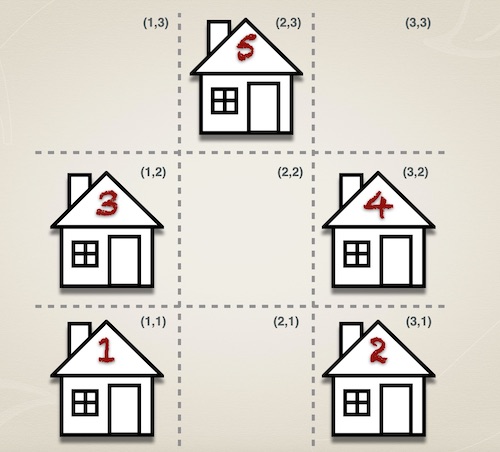
Here is the clp(fd) solution, most notably is the encoding of the house number and position pairs relation. While the Houses number is fixed, the Husbands and Wifes are the constrained variables, limited and distinct between 1..5, will be unified with the Houses number according to their spatial relations.
:- use_module(library(clpfd)). house_puzzle(Sol) :- Houses = [1,2,3,4,5], HousePos = [(1-1),(3-1),(1-2),(3-2),(2-3)], Husbands = [Adam,Bill,Lenny,Martin,Walter], HusbandNames = [adam,bill,lenny,martin,walter], Wifes = [Claire,Debbie,Katie,Mary,Sandra], WifeNames = [claire,debbie,katie,mary,sandra], pairs_keys_values(HusbandPairs, Husbands, HusbandNames), pairs_keys_values(WifePairs, Wifes, WifeNames), pairs_keys_values(HousePairs, Houses, HousePos), maplist(all_distinct,[Husbands,Wifes]), Husbands ins 1..5, Wifes ins 1..5, % 1. Claire lives further east than Walter, who isn't married to Mary. Claire #\= Walter, Mary #\= Walter, member(Claire-X1, HousePairs), member(Walter-X2, HousePairs), dif(X1,X2), eastof(X1,X2), % 2. Walter lives further west than Debbie, who lives further south than Bill. Debbie #\= Walter, Walter #\= Bill, member(Walter-X2, HousePairs), member(Debbie-X3, HousePairs), member(Bill-X4, HousePairs), dif(X3,X2), eastof(X3,X2), dif(X4,X3), northof(X4,X3), % 3. Sandra lives further north than Katie, who lives further east than Adam. Sandra #\= Adam, member(Sandra-X5, HousePairs), member(Adam-X6, HousePairs), member(Katie-X7, HousePairs), dif(X5,X7), northof(X5,X7), dif(X7,X6), eastof(X7,X6), % 4. Lenny lives further north than Martin. member(Lenny-X8, HousePairs), member(Martin-X9, HousePairs), dif(X8,X9), northof(X8,X9), % solution as a sorted [[husband,wife,house]. ] list house_solution(HusbandPairs,WifePairs,HousePairs,Sol). The house topological relations can be expressed as integer constraint with their corresponding X-Y coordinate pairs. If X1 coordinate is greater than X2 , the house position of X1-_ is further east of house position of X2-_ . Similarly, the Y coordinate is used to determine the north of houses relation.
eastof((X1-_),(X2-_)) :- X1 #> X2. northof((_-Y1),(_-Y2)) :- Y1 #> Y2. Finally, the house_solution/4 is the sorted integer keys of HusbandPairs, WifePairs and HousePairs values. Then write_list/1 is called to display the solution nicely as [husband, wife, house] tuples.
house_solution(HusbandPairs,WifePairs,HousePairs,Sol) :- maplist(keysort,[HusbandPairs,WifePairs,HousePairs],[HSort,WSort,XSort]), house_solution_(HSort,WSort,XSort,Sol). house_solution_([],[],[],[]). house_solution_([_-H|HTail],[_-W|WTail],[XK-_|XTail],[[H,W,XK]|NextSol]) :- house_solution(HTail,WTail,XTail,NextSol). write_list([First|Rest]) :- writeln(First), write_list(Rest). The house puzzle solution can be found (the last false means no more solution),
?- house_puzzle(Sol),write_list(Sol). [adam,mary,1] [martin,katie,2] [walter,sandra,3] [lenny,debbie,4] [bill,claire,5] false. You can learn more about clp(fd) from [MP18] [CLPFD-TUTOR]. In particular, learning directly from the author of clp(fd) on the subject of Puzzle Solving [POWER-PROLOG] is the best. I found the following tutorial videos are very enjoyable!
After all, I am totally in love with the Prolog’s constraint logic programming! Be warned, there is no turning back. :)
Content © 2016-2024 Benny Cheung. Subscribe via RSS.
Hosted on GitHub Pages. Design and code are open source: fork me, or open an issue.